アディムランドの教材の全般的な特質は、発達心理学をはじめ国語学・数学・論理学その他さまざまな分野の知見を根拠に、それら多様なコンセプトを教材に再構成しているところにあります。ここで、一例をあげてその過程をたどってみましょう。

足し算より引き算が難しいのはなぜか？ に解を見つけたい！
幼児に引き算をイメージさせるのは足し算よりはるかに難しいという現実があります。その要因を「幼児は、集合（クラス）における部分と全体を同時に把握できない」という心理学上の知見に求め、「解決」の道筋を探っているのが以下に掲げる一連の教材です。

心理学の泰斗、ピアジェの『新しい児童心理学』（J.ピアジェ他著・白水社刊クセジュ文庫・1,961年）に次のような記述があります（104ページ）。引用しましょう。論理的な説明のあとに具体例として提示されたものです。

たとえば、十二本の花からなる集合Bがあり、その下位集合Aとして六本のサクラソウが含まれているものについて、子どもに花BとサクラソウAとをかわるがわる指定させてみると、彼は正しく応答して、B全体およびその部分Aを指定できる。ところが、≪ここには花の方がたくさんあるのか、サクラソウの方がたくさんあるのか？≫と尋ねてみると、彼ははめこみA＜Bにしたがって反応することができない。それは、彼が部分Aを考え出すと、全体Bはひとつの単位として保存されなくなって、もはや、Aはその補集合A’としか比較しえなくなる（だから、彼は、≪同じ≫と答えたり、またサクラソウが七本ならサクラソウの方が多い、と言ったりするのだろう）からなのである。このようにもろもろのクラスを外延においてはめこむことは、八歳ごろにできるようになるものであり、また、操作的なクラス化を特徴づけるものである。

ここに「引き算の難しさ」があるのではないかと仮定し、この知見を解きほぐして課題に再編したの以下の教材です。いわば「知見への逆襲」ですね。

まず、【5538  どっちが多く囲んでる】ですが、ここには少しだけ「知見への逆襲」が忍び寄っています。

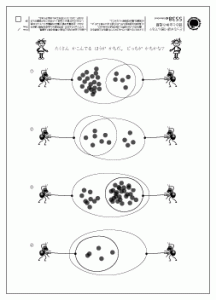
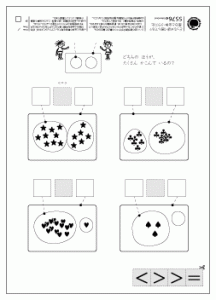
【 5576  どっちが多く囲んでる？】では、5538の要素をすでになじんだ集合のベン図にはめ込んで、AとB、つまり部分集合と全体集合のどちらが大きいかを、ビジュアルな図上で問うています。

また、【5718  りんごは残っているか？】では、同じ知見への解きほぐしを異なるアプローチでまさぐっています。
（三段論法の論理操作。賛否のあるピアジェの実験「都市Nの住民のいくらかはブルターニュ人である」「都市Nのブルターニュ人はすべて戦争で死んだ」「都市Nの住民は、まだ生き残っていたか」の課題を構成はそのままにより子どもに妥当な内容へアレンジしたものです。）

そして、【5936  全体集合と部分集合】では具象画と言語とをリンクさせ、部分集合と全体集合のどちらが大きいか問うています。クイズはいよいよ核心へと迫ります。

【6038  金魚と黒い金魚】では「知見への逆襲「」そのものがクイズとなっています。

このようなクイズを手を変え品を変え繰り返すことが「発達の最近接領域」に向けて有効なことがあります。成熟の平面に鍬を入れるような面白い試みだと評価をいただくことはありますが、簡単に答えが出るものではありません。ただ、少なくともこれらのクイズを好奇心をもって受け入れてくれる子がいること、誤答から正答に至る間に「なぜ引き算が難しいのか」を垣間見ることができること、などはご報告できます。